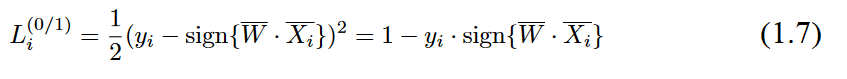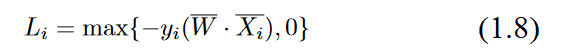What Objective Function Is the Perceptron Optimizing?

the original perceptron paper by Rosenblatt did not formally propose a loss function. In those years, these implementations were achieved using actual hardware circuits. The original Mark I perceptron was intended to be a machinerather than an algorithm, and custom-built hardware was used to create it. The general goal was to minimize the number of classification errors with a heuristic updateprocess (in hardware) that changed weights in the "correct" direction whenever errors weremade. This heuristic update strongly resembled gradient descent but it was not derivedas a gradient-descent method. Gradient descent is defined only for smooth loss functionsin algorithmic settings, whereas the hardware-centric approach was designed in a more heuristic way with binary outputs.





Many of the binary and circuit-centric principles were inherited from the McCulloch-Pittsmodel of the neuron. Unfortunately, binary signalsare not prone to continuous optimization. Can we find a smooth loss function, whose gradient turns out to be the perceptronupdate? The number of classification errors in a binary classification problem can be writtenin the form of a 0/1 loss function for training data point (X̄_i,y_i) as follows: The simplification to the right-hand side of the above objective function is obtained by setting both y²_i and sign {W̄.X̄_i}² to 1, since they are obtained by squaring a value drawn from{-1,+1}. However, this objective function is not differentiable, because it has a staircase-like shape, especially when it is added over multiple points. Note that the 0/1 loss above is dominated by the term -y_isign{W̄.X̄_i}, in which the sign function causes most ofthe problems associated with non-differentiability.



Since neural networks are defined bygradient-based optimization, we need to define a smooth objective function that is responsible for the perceptron updates. It can be shown that the updates of the perceptronimplicitly optimize theperceptron criterion. This objective function is defined by droppingthe sign function in the above 0/1 loss and setting negative values to 0 in order to treat all correct predictions in a uniform and loss less way:

you are encouraged to use calculus to verify that the gradient of this smoothed objective function leads to the perceptron update, and the update of the perceptron is essentially The modified loss function to enable gradient computation of a non-differentiable function is also referred to as a smoothed surrogate loss function. Almost all continuous optimization-based learning methods (such as neural networks) with discrete outputs (such as class labels) use some type of smoothed surrogate loss function

Although the aforementioned perceptron criterion was reverse engineered by working backwards from the perceptron updates, the nature of this loss function exposes some ofthe weaknesses of the updates in the original algorithm. An interesting observation about theperceptron criterion is that one can se W̄ to the zero vector irrespective of the training dataset in order to obtain the optimal loss value of 0. In spite of this fact, the perceptron updatescontinue to converge to a clear separator between the two classes in linearly separable cases;after all, a separator between the two classes provides a loss value of 0 as well. However,the behavior for data that are not linearly separable is rather arbitrary, and the resulting solution is sometimes not even a good approximate separator of the classes.

The direct sensitivity of the loss to the magnitude of the weight vector can dilute the goal of class separation; it is possible for updates to worsen the number of misclassifications significantly while improving the loss. This is an example of how surrogate loss functions might sometimes not fully achieve their intended goals. Because of this fact, the approach is not stable and can yield solutions of widely varying quality. Several variations of the learning algorithm were therefore proposed for inseparable data,and a natural approach is to always keep track of the best solution in terms of the number of misclassifications. This approach of always keeping the best solution in one's "pocket" is referred to as thepocket algorithm. Another highly performing variant incorporates the notion of margin in the loss function, which creates an identical algorithm to the linear support vector machine. For this reason, the linear support vector machine is also referred to as the perceptron of optimal stability.